Sous-programmes récursifs

Définition récursive

Dans une définition récursive ou par récurrence nous définissons une classe d’objets (ou de faits) très proches les uns des autres en fonction d’eux-mêmes. Une définition récursive met en jeu une base, où un ou plusieurs objets sont définis et une étape de récurrence où les objets de complexité supérieure sont définis en fonction des objets de la collection qui sont de moindre complexité.

Exemple 1 : La fonction factorielle :

Exemple 2 : La fonction puissance entière :

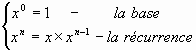
Sous-programmes récursifs

Un sous-programme récursif est un sous-programme appelé depuis son propre corps. Souvent l’appel est direct (il y a un appel direct à soi-même du corps du sous-programme), mais parfois il peut être indirect : une procédure P1 appelle directement une procédure P2 qui appelle directement P3 et ainsi de suite jusqu’à ce qu’une procédure Pk de la séquence appelle P1. En autres mots le sous-programme récursif est appelé avant que son exécution précédente est terminée.
 
Exemple 1 : Calcul de la fonction factorielle

L’algorithme récursive pour le calcul de la fonction factorielle est représenté par l’arbre suivant :

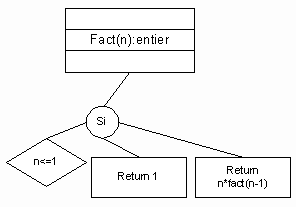
et la fonction Pascal :
 

Function Fact(n : integer):integer;
 Begin
  If n <= 1 Then
   Fact := 1
  Else
   Fact = n*Fact(n-1);
 End;
 
L’expression logique dans l’instruction If distingue le cas de base du cas de récurrence. Chaque appel récursif diminue la valeur du paramètre et de cette façon on va arriver inévitablement jusqu’au cas de base. Par exemple, si nous appelons fact(4), le résultat est un appel à Fact(3), qui appelle Fact(2), qui appelle Fact(1). A ce stade nous avons n<=1, donc Fact(1) applique la règle de base et retourne la valeur 1 à Fact(2). Cet appel à Fact terminel’instruction en retournant 2à Fact(3). A son tour Fact(3) retourn 6 à Fact(4) qui termine l’appelle et retourne 24 au programme appelant.
 
Phase d’appel Etat de la pile du programme Phase de retour
Appel ¯ ­ Retour 24
Fact(4)

Appel ¯

 Fact(4)

­ Retour 6
Fact(3)

Appel ¯

 Fact(3)

­ Retour 2
Fact(2)

Appel ¯

 Fact(2)

­ Retour 1
Fact(1) 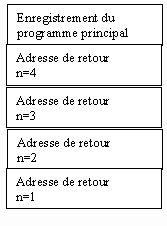Fact(1)

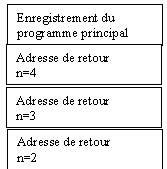
Chaque nouveau appel crée un enregistrement d’activation de la fonction Fact avec toutes ses variables locales (y compris les paramètres). Les sous-programmes récursifs gaspillent plus de mémoire que les sous-programmes itératifs. Donc il faut utiliser répétitives quand c’est possible comme dans l’exemple précédant.

Exemple 2 : Les tours de Hanoi.

C’est un jeu dans lequel on doit déplacer N disques qui sont enfilés sur un pal nommé source sur un autre appelé destinataire.. Chaque disque est couché sur un disque avec un plus grand diamètre. Il y a un autre pal vide –auxiliaire. On ne peut déplacer qu’un disque à la fois et on peut poser un disque sur un autre seulement si le dernier a un diamètre supérieur. Ici on peut définir la règle récurrente suivante:

BASE : S’il y a un disque sur le source on le déplace sur le destinataire.

 
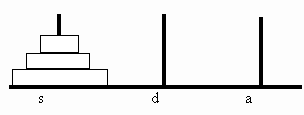
RECURRENCE : S’il y a N disques sur le source on déplace N-1 disques sur l’auxiliaire à l’aide de destinataire (qui est vide), puis on déplace N-ième disque (le plus grand) sur le destinataire et enfin les N-1 disques de l’auxiliaire sur le destinataire à l’aide du source (qui est déjà vide).

On peut maintenant écrire la procédure suivante :
 

Procedure Hanoi(N,s,d,a : integer);
{s,d,a sont pour source, destinataire et auxiliaire}
Begin
If n > 1 then Hanoi(N-1,s,a,d)
Writeln(‘Deplacer un disque de ‘,s,‘ sur ‘, d);
If n > 1 then Hanoi(N-1,a,d,s);
End;
 
Le tableau suivant montre le suite des appels et affichages, si l’appel initial est Hanoi(3,1,2,3)
 
N Appel ou affichage n s d a
  Hanoi(3,1,2,3) 3 1 2 3
  Hanoi(2,1,3,2) 2 1 3 2
  Hanoi(1,1,2,3) 1 1 2 3
  Affichage de 1 sur 2 1 1 2 3
  Retour de 3        
  Affichage de 1 sur 3 2 1 3 2
  Hanoi(1,2,3,1) 1 2 3 1
  Affichage de 2 sur 3 1 2 3 1
  Retour de 7        
  Retour de 2        
  Affichage de 1 sur 2 3 1 2 3
  Hanoi(2,3,2,1) 2 3 2 1
  Hanoi(1,3,1,2) 1 3 1 2
  Affichage de 3 sur 1 1 3 1 2
  Retour de 13        
  Affichage de 3 sur 2 2 3 2 1
  Hanoi(1,1,2,3) 1 1 2 3
  Affichage de 1 sur 2 1 1 2 3
  Retour de 17        
  Retour de 12        
  Retour de 1        

Exercises :

  1. Ecrivez une fonction pour calculer le PCGD de deux nombres entier m et n selon la définition suivante récursive qui suppose m>n:

    2. BASE : Si m est un multiple de n, alors n est le PGCD de m et n.
    RECURRENCE : Si m n’est pas un multiple de n, posons k le reste de la division m/n. Alors PGCD(m,n) est égale à PGCD(n,k).
    Prouvez que la définition récursive donne le même résultat que la définition non-récursive (le plus gran commun diviseur)
  2. Le nombre de combinaison de m choses parmi n s’écrit . Il y a une définition récursive :

    3. BASE : 
    RECURRENCE : Si 0<m<n, alors  .
    Ecrivez un programme réalisant cette définition et prouvez que la formule non-récursive :
donne le même résultat