EXERCICE V

Expressions et structures de contrôle de base (projet 1)

1. Calculer tous les nombres premiers qui sont inférieurs¸ à un nombre donné N et dont la présentation binaire est une séquence symétrique de zéros et uns (commençant par 1).

2. Afficher toutes les présentations d’un nombre N comme une somme de trois termes entiers. On ne tient pas compte aux permutations des mêmes termes.

3. Entrer N nombres entiers. Afficher ce nombre qui a un nombre maximal de uns (1) dans sa présentation binaire.

4. Calculer les valeurs de la fonction F(x) = 2 sin(x) - cos(x) pour tous les x dans l’intervalle [0.,1.] et Dx = 0.1
Ranger les résultats dans un tableau.

5. Entrer N nombres entiers et n’afficher que ceux dont les numéros de positions des zéros dans la présentation binaire forment une progression arithmétique.

6. Afficher le nombre entier qui parmi tous les nombres premiers dans un intervalle donné a un nombre maximal d’uns (1) dans sa représentation binaire.

7. Ecrire un programme qui calcule la racine cubique, en utilisant la formule : , ou α et β sont deux approximations consécutives vers (β est meilleure approximation).

8. Ecrire un programme qui calcule la somme de la série : dans les deux directions.(n et x sont donnés). Comparer les résultats.

9. Ecrire un programme qui calcule la somme de la série : dans les deux directions.(n et x sont donnés). Comparer les résultats.

10. Ecrire un programme qui calcule la somme de la série : dans les deux directions.(n et x sont donnés). Comparer les résultats.

11. Afficher tous les nombres entiers inférieurs à N, qui se divisent à tous ses chiffres.

12. Afficher tous les nombres premiers pairs (inférieurs à N) dont les présentations ternaires sont obtenues une de l’autre par inversion.

13. Trouver tous les nombres entiers (inférieurs à N) dont la représentation décimale est une suite croissante ou décroissante de chiffres.

14. Entrer une somme initiale, l’intérêt mensuel, le nombre de mois, et calculer l’intérêt total et la somme dans la fin de chaque mois pour une compte bancaire.

15. Ecrire un programme qui calcule la somme de la série : avec une exactitude ε donné pour tous les x dans l’intervalle [x_d,x_f.] avec un incrément Δx.

16. Ecrire un programme qui calcule la somme de la série : avec une exactitude ε donné pour tous les x dans l’intervalle [x_d,x_f.] avec un incrément Δx.

17. Ecrire un programme qui additionne deux nombres rationnels présentés comme binôme de nombres entiers.

18. Afficher le nombre entier qui parmi tous les nombres impairs dans un intervalle donné a un nombre maximal de trois dans sa représentation octale.

19. Afficher le nombre entier qui parmi tous les nombres pairs dans un intervalle donné a une somme maximale des chiffres dans sa représentation octale.

20. Ecrire un programme qui lit des nombres entiers jusqu’à 0 soit lu et affiche la somme de leurs chiffres dans la représentation décimale.

21. Ecrire un programme qui lit des nombres réels jusqu’à 0 soit lu et affiche les moyennes des nombres positifs et négatifs respectivement.

22. Ecrire un programme qui lit des nombres entiers jusqu’à 0 soit lu et affiche ce nombre qui parmi tous les nombres pairs a une somme maximale des chiffres dans sa représentation ternaire.

23. Afficher le nombre entier qui parmi tous les nombres pairs dans un intervalle donné a un nombre maximal de deux dans sa représentation octale.

24. Ecrire un programme qui lit des nombres réels jusqu’à la fin du fichier soit atteint et affiche les sommes des nombres positifs et négatifs respectivement.

25. Ecrire un programme qui lit des nombres entiers jusqu’à la fin du fichier soit atteint et affiche la somme de tous les nombres divisibles à trois.

26. . Ecrire un programme qui lit des nombres entiers jusqu’à la fin du fichier soit atteint et affiche les somme de chiffres de tous les nombres divisibles à cinq.

27. Affichez un triangle isocèle formé d'étoiles de N lignes (N est fourni au clavier):
Nombre de lignes : 8

*
***
*****
*******
*********
***********
*************
***************

28. Affichez un triangle formé d'étoiles de N lignes (N est fourni au clavier):
 *
 **
 ***
 ****
 *****
 ******
 *******
 ********
 *********
 **********

29. Calculez pour une valeur X donnée du type float la valeur numérique d'un polynôme de degré n:
P(X) = A_nXⁿ + A_n-1X^n-1 + ... + A₁X + A₀
Les valeurs de n, des coefficients A_n, ... , A₀ et de X seront entrées au clavier.
Utilisez le schéma de Horner qui évite les opérations d'exponentiation lors du calcul:

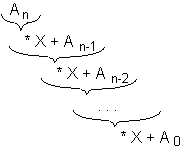
30. Calculez par multiplications successives X^N de deux entiers naturels X et N entrés au clavier.

31. Lire des nombres jusqu'à ce que la somme des nombres lus soit égale à un nombre demandé au préalable à l'utilisateur. Signaler combien, parmi les nombres lus, étaient strictement positifs, strictement négatifs et égaux à 0.

32. Lire des nombres jusqu'à trouver un nombre demandé au préalable à l'utilisateur à condition que ce nombre soit égal à la somme des deux derniers nombres lus juste avant lui.

33. Lire des nombres jusqu'à trouver trois multiples de 5. En fin de programme, afficher les 3 multiples rencontrés dans l'ordre de leur lecture.

34. Lire des nombres jusqu'à trouver 5 multiples d'un nombre demandé au préalable à l'utilisateur. Signaler, parmi ces 5 multiples, combien étaient également des nombres pairs. Afficher le nombre de 0 rencontrés.

35. Lire des nombres en demandant au préalable à l'utilisateur combien de nombres seront à lire. En fin de lecture, afficher le plus petit et le plus grand nombre de la liste.

Page precedente Page suivante Sommaire