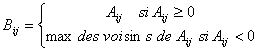1.
Soit une suite A avec N
éléments est donnée. Trouver la valeur maximale des
éléments négatifs. Utiliser une fonction.
2.
Soit une matrice B(N,N). Trouver
la somme des éléments qui sont posés au-dessous de la
diagonale complémentaire. Utiliser une fonction.
3.
Soit une matrice carrée
X(N,N). Trouver la somme des éléments qui sont posés dans
le triangle hachuré. Utiliser une fonction. 
4.
Soit une matrice carrée
X(N,N). Trouver la moyenne des éléments qui sont posés
dans le triangle hachuré. Utiliser une fonction. 
5.
Soit une matrice carrée
X(N,N). Trouver la somme des éléments qui sont posés dans
le triangle hachuré. Utiliser une fonction. 
6.
Soit une matrice carrée
X(N,N). Trouver la moyenne des éléments qui sont posés dans
le triangle hachuré. Utiliser une fonction. 
7.
Soit une suite A avec N (N £ 50) éléments
entiers. Trouver la valeur maximale des éléments pairs. Utiliser
une fonction.
8.
Trouver la moyenne des
éléments avec deux indices pairs de la matrice B(M,N). Utiliser
une fonction.
9.
Soit une suite LINDA avec N (N £ 20) éléments
entiers. Trouver la valeur maximale des éléments impairs.
Utiliser une fonction.
10.
Soit une matrice B(N,N). Trouver
le produit des éléments qui sont posées au-dessous de la
diagonale complémentaire et dont la valeur est entre 0 et 3. Utiliser
une fonction.
11.
Soit une suite MAS avec N (N £ 20) éléments
entiers. Afficher tous les éléments divisibles à trois.
Utiliser une fonction.
12.
Soit une suite X avec N
éléments réels. Trouver la valeur et la place de
l’élément maximal parmi les éléments
inférieurs à 2,1. Utiliser une fonction.
13.
Trier une suite A ayant longueur N
(N £ 20) en ordre
décroissant. Utiliser une fonction.
14.
Trouver les éléments
maximales de chaque ligne d’une matrice B(M,N). Utiliser une fonction.
15.
Trouver la somme des éléments
d’une matrice carrée Q(N,N) qui se trouvent sur et au-dessous de la
diagonale principale. Utiliser une fonction.
16.
Dans une matrice D(M,M) trouver
l’élément maximal parmi les éléments minimaux de toutes
les lignes parallèles à la diagonale principale. Utiliser une
fonction.
17.
Dans une matrice A(M,N) trouver
l’élément minimal parmi les éléments maximaux de
toutes les lignes. Utiliser une fonction.
18.
Une matrice carrée C(N,N)
est donnée. Trouver le produit des éléments qui sont
posées dans le triangle hachuré et dont la valeur est entre 0 et
3.  Utiliser une fonction.
Utiliser une fonction.
19.
Une matrice X(N,M) est
donnée. Afficher ces éléments dans l’ordre suivant . Utiliser une fonction.
. Utiliser une fonction.
20.
Trier une suite entière A ayant
longueur N (N £ 20) en ordre suivant :
d’abord tous les nombres impairs en ordre croissant et puis tous les nombres
pairs en ordre décroissant. Utiliser une fonction.
21.
Trouver les éléments
maximales de chaque colonne d’une matrice B(M,N). Utiliser une fonction.
22.
Trouver le nombre d’éléments qui
se trouvent entre l’élément minimal et l’élément
maximal d’une suite B ayant longueur N (N £ 50).
Utiliser une fonction.
23.
Echanger les places des éléments
minimal et maximal dans une matrice
B(M,N). Utiliser une fonction.
24.
Une matrice A(N,N) est
donnée. Calculer une nouvelle matrice B, dont les valeurs sont :
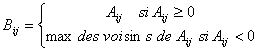
25.
Une matrice X(N,M) est
donnée, N <= 7, M <= 10. Trouver la somme des éléments dont la somme des indices
est paire.
26.
Une matrice carrée X(N,N)
est donnée. Trouver la somme des éléments positifs qui
sont posés dans le triangle hachuré. 
27.
Trouver l’élément
minimal parmi ces qui se trouvent sur les deux diagonale d’une matrice
carrée.
28.
Ecrire un programme qui lit un
texte (jusqu’à 80 caractères) et calcule le nombre d’occurrences
de chaque caractère.
29.
Ecrire un programme qui lit un
texte (jusqu’à 80 caractères) et calcule le nombre de signes de
ponctuation.
30.
Ecrire un programme qui lit un
nombre au format õõõõ<óóó>, où «xxxx» est la représentation du nombre dans le
système de base «yyy» et l’affiche en système décimal.
31.
Ecrire un programme qui lit deux
dates au format dd/mm/yyyy
et calcule la plus récente.
32.
Lire les taux de change de 5
devises de base et calculer toutes les parités d’échange.
33.
Ecrire une fonction qui recherche
le nombre d’éléments qui se trouvent entre
l’élément maximal et l’élément minimal d’un tableau
unidimensionnel. Lire un tableau unidimensionnel ALFÀ(N), N<=20 et trouver le nombre
d’éléments qui se trouvent entre ses éléments
maximal et minimal
34.
Ecrire une fonction qui trie les
éléments d’un tableau unidimensionnel en ordre croissant. Lire le
tableau bidimensionnel A(N,M), N<=10, M<=15 et trier ses
éléments par colonnes.
35.
Ecrire une fonction qui trouve le
radius de cercle inscrit d’un triangle déterminé par les
coordonnées de ses sommets. Afficher la valeur du le radius de cercle
inscrit du triangle qui a pour sommets les points (-4., -4.), (5., 1.), (-3., 4.).
36.
Ecrire une fonction qui trouve
l’élément minimal d’un tableau unidimensionnel. Lire le tableau
bidimensionnel A(N,M), N<=15, M<=15 et trouver l’élément
maximal parmi les minimums de ses lignes.
37.
Ecrire une fonction qui trie les
éléments d’un tableau unidimensionnel en ordre
décroissant. Lire le tableau bidimensionnel A(N,M), N<=10, M<=15
et trier ses éléments par lignes.
38.
Ecrire une fonction qui trie les
éléments d’un tableau unidimensionnel en ordre croissant. Lire le
tableau bidimensionnel A(N,M), N<=10, M<=15 et trier ses
éléments par lignes.
39.
Ecrire une fonction qui trouve les
hauteurs d’un déterminé par les coordonnées de ses
sommets. Afficher la valeur de la hauteur minimale du triangle qui a pour
sommets les points (-4., -4.), (5.,
1.), (-3., 4.).
40.
Ecrire une fonction qui trouve la
surface d’un triangle déterminé par les coordonnées de ses
sommets. Lire les coordonnées des sommets de trois triangles et calculer
la somme de leur surfaces.
41.
Ecrire une fonction qui trouve les
chiffres d’un nombre en système N-aire. Lire un nombre et trouver ses
chiffres en systèmes binaire, octal et hexadécimal.
42.
Ecrire une fonction qui calcule la
longueur de la bissectrice maximale d’un triangle déterminé par
les coordonnées de ses sommets.
Lire les coordonnées des sommets de N triangles et trouver le
triangle avec la plus courte bissectrice maximale.
43.
Ecrire de sous-programmes qui
réalisent l’arithmétique vectorielle (addition, soustraction,
produit vectoriel etc.). lire deux vecteurs et les subir à tous les
opérateurs réalisés.
44.
Ecrire une fonction qui trie les
éléments d’un tableau unidimensionnel en ordre
décroissant. Lire le tableau bidimensionnel A(N,M), N<=10, M<=15
et trier ses éléments par colonnes.
45.
Ecrire une fonction qui calcule le
produit des éléments d’un tableau unidimensionnel pris avec un
pas. . Lire le tableau bidimensionnel G(N,M), N<=15, M<=12 et trouver le
produits d’élément de la chaque lignes pris avec un pas X.
46.
Ecrire une fonction qui calcule la distance
entre un point et une droite. Lire les coordonnées de trois points et
calculer la distance entre le premier point et la droite qui passe par les autres.
47.
Ecrire une fonction qui trouve les
hauteurs d’un triangle déterminé par les coordonnées de
ses sommets. Afficher la valeur de la hauteur minimale du qui a pour sommets
les points (-2., -4.), (5., 2.), (-3., 4.).
48.
Ecrire une fonction qui calcule la distance
entre deux points déterminés par leurs coordonnées. Lire
les coordonnées de cinq pairs de points et calculer la distance chaque
pair.
49.
Ecrire une fonction DIGIT qui trouve les chiffres
d’un nombre entier dans un tableau. Déterminer si les chiffres d’un
nombre se trouvent dans un autre. Les deux nombres ont 5 chiffres chacun.
50.
Un véhicule tout terrain
peut passer 500 km avec un plein. D’un entrepôt initial qui contient
essence pour N pleins le véhicule peut passer en créant des
entrepôts temporels:
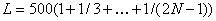 km
km
Ecrire une fonction qui calcule N en fonction de L. Ecrire un programme qui
affiche combien d’essence et combien d’entrepôts sont nécessaires
afin le véhicule puisse passer un désert dont la longueur est M
km.
51.
Ecrire une fonction qui calcule la
somme de deux vecteurs représentés comme des tableaux
unidimensionnels. Lire les donnés de 5 vecteurs et trouver leur somme.
52.
Ecrire une fonction qui calcule la
distance entre deux points déterminés par leurs
coordonnées. Lire les coordonnées de N points (M≤50) et
calculer la distance maximale entre n’importe quel binôme.
53.
Ecrire une fonction qui trouve les
bissectrices d’un triangle déterminé par les coordonnées
de ses sommets. Afficher la valeur de la bissectrice maximale du triangle qui a
pour sommets les points (-4., -4.),
(5., 1.), (-3., 4.).




 Utiliser une fonction.
Utiliser une fonction. . Utiliser une fonction.
. Utiliser une fonction.