----->(a+b)/(c+d) Les expressions et l'affectation
Les expressions permettent de préciser les calculs à effectuer à l'aide d'opérateurs à partir des valeurs de variables et de constantes. Les valeurs obtenues peuvent être rangées dans les variables par l'instruction d'affectation. Chaque expression a un type qui dépend des opérandes et l'opérateur en jeu; c'est le type du résultat.
Les expressions peuvent être complexes et utiliser
plusieurs opérateurs. Par la priorité d'opérateur
le langage précise dans quel ordre les opérations doivent
se faire. Quand deux opérateurs ont la même priorité
le calcul s'effectue de gauche à droite.
Elles produisent un résultat entier ou réel. Les opérateurs sont:
| Nom | Opérateur | Priorité | Résultat |
| Moins unaire | - | 4 | Change le signe de son opérande. Il a le type d'opérande |
| Multiplication | * | 3 | Le type est réel, sauf si les deux opérandes sont entiers - alors le type est entier. |
| Division | / | 3 | Le type est toujours réel |
| Division entière | div | 3 | Les opérandes et le type du résultat sont entiers. |
| Reste | mod | 3 | Les opérandes et le type du résultat sont entiers. |
| Addition | + | 2 | Le type est réel, sauf si les deux opérandes sont entiers - alors le type est entier. |
| Soustraction | - | 2 | Le type est réel, sauf si les deux opérandes sont entiers - alors le type est entier. |
On peut utiliser des parenthèses () pour gérer l'ordre des opérations: (a+b)*c et a+b*c. résultats. L'appel peut être écrit au lieu d'un opérande. Les arguments sont toujours entre parenthèses.
Exemple: a + SIN(b)
Les appels de fonction sont utilisés pour obtenir des résultats. Le (les) paramètre(s) de la fonction est (sont) toujours entre paranthèses.
Liste des fonctions arithmétiques:
| ABS(entier ou réel) | valeur absolue |
| SQR(entier ou réel) | carré |
| SUCC(entier ou comptable) | successeur (valeur suivante) |
| PRED(entier ou comptable) | prédécesseur (valeur précédente) |
| SQRT(réel0) | racine carrée |
| SIN(réel) | sinus |
| COS(réel) | cosinus |
| ARCTAN(réel) | arcus tangente |
| EXP(réel) | exponentielle exp(x)=ex |
| LN(réel>0) | logarithme népérien |
| TRUNC(réel) | la partie entière |
| ROUND(réel) | un entier arrondi |
Exemples:
----->(a+b)/(c+d)
------->
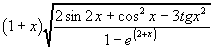(1+x)*SQRT((2*SIN(2*x)+SQR(COS(x)) - 3*SIN(SQR(x))/COS(SQR(x)))/(1-EXP(2+x)))
Le résultat de ces expressions est de type booléen.
C'est un test, dont le résultat peut être vrai ou faux.
La plus simple des expressions booléennes est la relation, dont
la syntaxe est:
<expr.arithm.><opérateur de relation><expr.arithm.>
Les opérateurs de relation sont:
< >
<= >= = <>
Le résultat est vrai ou faux selon que la relation
est vraie ou fausse.
a < 5 b>=
9.5 a+b
<>c/d
La priorité des opérateurs de relation est la plus basse (1).
Opérateurs booléens:
| Nom | Opérateur | Priorité | Résultat |
| Négation | not | 4 | Négation de l'opérande (not true = false). |
| Intersection logique | and | 3 | Vrai si et seulement si les deux opérandes sont vrais. |
| Union logique | or | 2 | Faux si et seulement si les deux opérandes sont faux. |
| Union logique | xor | 2 | Vrai si mais seulement si un des opérandes est vrai. |
Tableau de vérité
|
a |
b |
not b |
a and b |
a or b |
a xor b |
|
F |
F |
T |
F |
F |
F |
|
F |
T |
F |
F |
T |
T |
|
T |
F |
T |
F |
T |
T |
|
T |
T |
F |
T |
T |
F |
Exercices:
La syntaxe est:
<variable> := <expression>
L'expression est calculée et sa valeur est rangée dans la variable. L'expression doit être de type compatible avec celui de la variable. C'est le cas quand elles sont du même type ou quand l'expression est entière et la variable réelle. Mais quand la variable est entière et l'expression réelle il faut utiliser "trunc" ou "round" pour transformer la valeur réelle à une valeur entière.
Exemples:
Si on a les déclarations:
Var
x,a : Real; d: boolean; k : char; b : integer;
ce sont des affectations légales:
x := a + 5*b/(x-1);
d : = b=0;
k := ';'